The Golden Ratio in Layman's Terms

The Golden Ratio is one of those concepts that is so incredible in its properties, presence, and applicability that the concept of it can easily overwhelm people. One hears the word "ratio of A to B is..." and proceeds to zone out, not hearing the rest, and not caring. But we students of architecture do not have this luxury. The Golden Ratio is as fundamental to our would-be occupation as knowledge of heat and timing is to a cook. Some architecture does exist that does not use the Golden Ratio, just as some cooking does not use a stove or oven, but knowing its use is more or less required knowledge to be able to discuss and appreciate architecture.

What is a Ratio?

So let's start at the most fundamental part. By "ratio" we mean how one thing compares to another. Let's start off simple...

The ratio of 10 to 30 is 1:3

This is not the Golden Ratio, it is merely a simple ratio to explain how ratio plays a part before we get into the specifics of how a ratio can be "Golden".

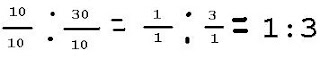The ":" is a shorthand way of expressing "(the amount on the left) compared to (the amount on the right)". You find this by figuring out what the greatest common denominator is (10), and dividing both numbers by it. Then simplify both sides. The result is 1:3. What this means is that your small and large amounts will always be proportional to one another in this way.

If you wanted a rectangle that was proportional to a 1:3 ratio, it's sides could be 1x3, or 2x6, or 3x9, 4x12...10x30...50x150... notice how the number on the right is always three times the number on the left.

If you wanted a triangle that was proportional to a 1:3 ratio, your sides could be 1x1x3 or 3x3x1, or alternately you might decide to use a 1:3 angle for the ratio. Since a triangle's three inner angles must always total 180, if you wanted each angle to be at a 1:3 ratio from the other angles, then you would use a ratio of 1:3:9 (the "3" is three times 1, and one third of 9).

This can be solved via simple equation. Since your base unit (x) is the one all your other units in the ratio will be based off of, you can set up your equation entirely in terms of "x"

x+3x+9x=180
13x=180
x=180/13
x=13.84615...
3x=41.538461...
9x=124.615384...

So your triangle should have angles of roughly 14, 41, and 125. I realize the rounding is off on the 42, but all three angles must equal exactly 180, and even rounding to the nearest hundredth yields only a near-180 sum.

But it also brings up a very valid point: unless you have an extremely precise and accurate need for the Golden Ratio, it does not have to get down into real life measurements of fractions of millimeters. The intent will be easily enough recognized by other architects, and will be harmoniously felt by non-architects.

So what makes a ratio "Golden?"

The idea is actually much simpler than the math behind it.

Instead of using specific numbers, let's use variables "a," "b," and "c" for the ratios.

So any two-amount ratio can now be expressed simply as a:b

In a Golden Ratio, "a," "b," and their total, "a+b" all have a special relationship to one another. The shorter amount has the same ratio to the larger amount as the larger amount has to the total of both amounts.

For example, here is a line divided into two different lengths, "a," and "b,".

If the segment is golden, then the ratio of a to b should be the same as the ratio of b to the total of "a plus b", or expressed mathematically

a:b = b:(a+b).

A visual representation of this would be something like this:
a:b:(a+b)

Sounds simple? The concept is very simple. However, the mathematical properties behind it are incredible. For the purposes of architecture I'm only going to go into a couple of them.

First, to simplify things, the mathematical symbol for the Golden Ratio is lower-case phi (φ). The uppercase form (Φ) is used for the reciprocal of the golden ratio of 1/φ.

The variable equation for the Golden Ratio is:

But realistically, if you want to figure out what the Golden Ratio is on the fly, you need to multiply it by the numerical value.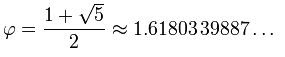

If you just want "quick," it's probably okay to simply use 1.618, or even 1.6. If you want "good," or precise and accurate, then you need to multiply your base value by (1+√5)/2 to obtain a larger amount that creates a golden ratio to your base value. Alternately, you can use the reciprocal and multiply your base value by 1/((1+√5)/2)) to obtain a smaller amount that has a golden ratio to your base amount.

Interestingly enough, the difference between the irrational number values of φ and its reciprocal Φ is exactly 1. So an easy way to keep them straight is to remember if you have a base value and want to go larger up the Golden scale, multiply by 1.618... and if you want to go smaller down the Golden Scale then multiply by 0.618...

Now, the uses for the Golden Scale are nearly endless, but where you'll find the most common use is in the use of rectangles and squares.

If you want to create a rectangle that is in Golden Scale to a base cube, you would do the following:

1. Start with a square (the red area).
2. Divide it in half.
3. Draw a diagonal from one of the corners created by the division, to the corner of the original square.
4. Use a compass to arc it around, then extend the wall of your square towards the arc until it intersects. The total length of that line, from the intersection to the opposite side of the square, is in Golden Ratio to the original side of the square.
5. Simply use this new line as the long side of your new rectangle, and the width of your square as the short side of the rectangle, and you now have a rectangle that is golden proportion to your square.
6. Alternately, you could use the new line as the value to make another square, and have two squares in golden proportion to one another, as I have illustrated below.

Notice how this is not a linear progression upwards, but rather a half-parabola.

The Fibonacci Connection:

Lastly, it's important to know the relationship between a Fibonacci series and the Golden Ratio. In short, the Fibonacci Sequence is derived by adding the two previous numbers to arrive at the next one. For instance:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, …

0+1=1, then 1+1=2, then 1+2=3, then 2+3=5, then 3+5=8, etc...

As these numbers get larger, the relationship between any two adjacent numbers in the sequence approaches the Golden Ratio. Try it and see...

8/5 = 1.6
13/8 = 1.625
21/13 = 1.615
34/21 = 1.619
55/34 = 1.617647...
89/55 = 1.618181...

As previously mentioned, since in Architecture, the intent and approximation of the Golden Ratio are more important than the exactness of the numbers, the Fibonacci sequence provides a convenient set of Golden Ratio numbers to use.

However, one is certainly not limited by that Fibonacci Sequence. Instead, one might decide to start with a base of any number, multiply it by phi, then take the result and multiply it by phi, and immediately, a new Fibonacci series becomes apparent...

10*(1.618)=16.18
16*(1.618)=26.179...
26*(1.618)=42.358...

10, 16, 26, 42...
(10+16=26), (16+26=42)...etc...

So the Golden Ratio and Fibonacci Series are intimately associated with one another.

a Fibonacci Golden Spiral

There are countless other odd relationships and facts that make the Golden Ratio interesting to not just architects, but also mathematicians, physicists, biologists, artists, musicians, and every other walk of the higher arts and sciences. It is little wonder that it should play such an important role in an architect's education. Though some architects, like Frank Gehry, eschew the Golden Ratio in their own works, the same way a cook might forswear the oven and stove in favor of the grill or the fire pit, the essential knowledge of it is vital to our occupation.